Inhalt
- Lineare Regression mit der diskreten Fehlerquadratmethode von Gauß
- Potenzielle Regression
- Logarithmische Regression
- Exponentielle Regression
- Trendlinie mit Excel
- Java-Kommandozeilenprogramm zur Ermittlung der Parameter von Approximationsfunktionen
- Beispiele für Approximationsfunktionen
- Einige häufig benötigte Formeln
Lineare Regression mit der diskreten Fehlerquadratmethode von Gauß
Für eine Menge von x-/y-Wertepaaren sollen die Parameter a und b gefunden werden zu der Approximationsfunktion
y = a + b * x.
Die theoretischen Grundlagen zur linearen Regression mit der diskreten Fehlerquadratmethode von Gauß ("Least-squares Fit")
finden Sie zum Beispiel erklärt unter:
http://www.mathe-online.at/nml/materialien/SkriptumBlaha/KAP-11.pdf,
http://www.scribd.com/doc/965028/MaSt-Statistik-2007 und
http://www.xuru.org/rt/toc.asp.
Folgendermaßen werden die Parameter a und b der linearen Regression berechnet:
| n | Anzahl der x-/y-Wertepaare |
| ∑x | Summe über alle x-Werte |
| ∑x2 | Summe über alle quadrierten x-Werte |
| ∑x*y | Summe über alle Produkte zusammengehörender x- und y-Werte |
| xm = ∑x / n | Arithmetischer Mittelwert der x-Werte ("Mean", "Average") |
| ym = ∑y / n | Arithmetischer Mittelwert der y-Werte ("Mean", "Average") |
| xv = ∑x2 / n - xm2 | Varianz der x-Werte ("Variance") (die Wurzel davon ist die "Standardabweichung") |
| yv = ∑y2 / n - ym2 | Varianz der y-Werte ("Variance") (die Wurzel davon ist die "Standardabweichung") |
| kv = ∑x*y / n - (xm * ym) | Kovarianz der x- und y-Werte |
| r2 = kv2 / ( xv * yv ) | Bestimmtheitsmaß ("Coefficient of Determination") (0...1, höher = besser)
(das Bestimmtheitsmaß ist das Quadrat des "Korrelationskoeffizienten") |
| b = kv / xv | Steigung der linearen Regression ("Slope") |
| a = ym - b * xm | Versatz der linearen Regression ("Intercept", "Offset") |
| y = a + b * x | Approximationsfunktion (Näherungsformel) der linearen Regression |
Wenn für verschiedene Arten von Approximationsfunktionen das Bestimmtheitsmaß r2 ("Coefficient of Determination") berechnet wird,
kann darüber entschieden werden, welches Näherungsverfahren besser geeignet ist (das mit dem höheren Wert).
Potenzielle Regression (Geometrische Regression, Power Regression)
|
Für eine Menge von x-/y-Wertepaaren sollen die Parameter α und β gefunden werden zu der approximierten Potenzfunktion:
y = α * xβ
Um die lineare Regression anwenden zu können, wird die Potenzfunktion umgeformt, so dass sie einer linearen Gleichung ähnelt:
ln(y) = ln(α) + β * ln(x)
Wenn in den obigen Formeln für die lineare Regression statt der x- und y-Werte jeweils die ln(x)- und ln(y)-Werte eingesetzt werden
und a und b der linearen Regression ermittelt werden, gilt:
| α = ea | (a über lineare Regression ermittelt) |
| β = b | (b über lineare Regression ermittelt) |
| y = α * xβ | Approximationsfunktion der potenziellen Regression |
|

|


|
Logarithmische Regression (Logarithmic Regression)

Für eine Menge von x-/y-Wertepaaren sollen die Parameter a und b gefunden werden zu der approximierten logarithmischen Funktion:
y = a + b * ln(x)
Wenn in den obigen Formeln für die lineare Regression statt der x-Werte jeweils die ln(x)-Werte eingesetzt werden,
können die Parameter a und b der Approximationsfunktion der logarithmischen Regression ermittelt werden.
|
Exponentielle Regression (Exponential Regression)

Standard-Exponentialfunktion
Für eine Menge von x-/y-Wertepaaren sollen die Parameter α und β gefunden werden zu der approximierten Exponentialfunktion
y = α * e(β * x) (oder alternativ
y = α * 10(β * x)).
Um wieder die lineare Regression anwenden zu können, wird die Exponentialfunktion umgeformt, so dass sie einer linearen Gleichung ähnelt:
ln(y) = ln(α) + β * x
Wenn in den obigen Formeln für die lineare Regression statt der y-Werte jeweils die ln(y)-Werte eingesetzt werden
und a und b der linearen Regression ermittelt werden, gilt:
| α = ea | (a über lineare Regression ermittelt) |
| β = b | (b über lineare Regression ermittelt) |
| y = α * e(β * x) | Approximationsfunktion der exponentiellen Regression |
|
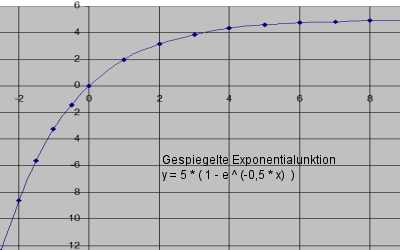
Gespiegelte und verschobene Exponentialfunktion
Schwieriger ist die Approximation der folgenden Exponentialfunktion, bei der die y-Werte bei 0 beginnen und dann gegen den Grenzwert α streben
(was bei vielen physikalischen Vorgängen zu beobachten ist):
y = α * (1 - e(-β * x))
Hierzu gibt es verschiedene Vorschläge für iterative Verfahren:
Zum Beispiel indem ausgehend von einer ersten Annahme für α die exponentielle Regression durchgeführt wird und
anschließend der α-Wert iterativ genauer ermittelt wird.
Bei den einzelnen Iterationen wird jeweils das Bestimmtheitsmaß berechnet, um in der richtigen Richtung fortzufahren.
Als erste Annahme für α kann zum Beispiel einfach ein etwas höherer Wert als der höchste bekannte y-Wert genommen werden.
Um für einen angenommenen α-Wert die beschriebene exponentielle Regression anwenden zu können,
müssen die x- und y-Werte vorher umgerechnet werden:
"x = -x" und
"y = α - y".
|
Trendlinie mit Excel
Folgendermaßen können Sie in einer Excel-Tabelle zu gegebenen Werten eine Trendlinie hinzufügen:
- Markieren Sie Ihre Daten in der Excel-Tabelle.
- Wählen Sie: 'Einfügen' | 'Diagramm...' | 'Punkt (XY)' | Klick auf mittleres Kurvendiagramm | 'Fertigstellen'.
- Klicken Sie mit der rechten Maustaste auf einen der Diagrammpunkte und wählen Sie: 'Trendlinie hinzufügen...'.
- Wählen Sie im Tabulatorreiter 'Typ' eine geeignete Approximationsfunktion:
'Linear', 'Logarithmisch', 'Polynomisch', 'Potenziell', 'Exponentiell' oder 'Gleitender Durchschnitt'.
- Aktivieren Sie im Tabulatorreiter 'Optionen':
'Gleichung im Diagramm darstellen' und 'Bestimmtheitsmaß im Diagramm darstellen'.
- 'OK'.
Java-Kommandozeilenprogramm zur Ermittlung der Parameter von Approximationsfunktionen
Das folgende Programm realisiert die oben erläuterten Regressionsverfahren:
import java.util.*;
public class Approximationsfunktionen
{
private static final int SP = 4;
public static void main( String[] args )
{
System.out.println( "Approximationsfunktionen zur Inter- und Extrapolation\n" +
"Kommentare siehe:\n" +
"http://www.torsten-horn.de/techdocs/java-approximationsfunktionen.htm" );
if( args == null || args.length < 2 || args.length % 2 != 0 )
{
System.out.println( "\nBitte eine Menge an x-/y-Wertepaaren angeben " +
"(Werte durch Leerzeichen getrennt)." );
return;
}
double[] xyArr = convertStringArrToDoubleArr( args );
ArrayList<RegressionResult> result = new ArrayList<RegressionResult>();
// Verschiedene Regressionen:
result.add( calculateLinearRegression( xyArr ) );
result.add( calculatePowerRegression( xyArr ) );
result.add( calculateLogarithmicRegression( xyArr ) );
result.add( calculateExponentialRegression( xyArr ) );
result.add( calculateOneMinusExponentialRegression( xyArr ) );
boolean atLeastOne = false;
for( Iterator<RegressionResult> itr = result.iterator(); itr.hasNext(); ) {
RegressionResult res = itr.next();
atLeastOne |= res != null;
if( res != null ) System.out.println( "\n" +
linksbuendigerString( res.titel + ":", " " ) +
linksbuendigerString( res.formel, " " ) +
" (Bestimmtheitsmass = " + res.rr + ")" );
}
if( atLeastOne ) {
System.out.print( "\nx y " );
for( Iterator<RegressionResult> itr = result.iterator(); itr.hasNext(); ) {
RegressionResult res = itr.next();
if( res != null ) System.out.print(
linksbuendigerString( res.titel, " " ) );
}
System.out.println();
for( int i=0; i < args.length && i < 20; i+=2 ) {
System.out.print( linksbuendigerString( "x=" + args[i] + ",", " " ) +
linksbuendigerString( " y=" + args[i+1] + ":", " " ) );
for( Iterator<RegressionResult> itr = result.iterator(); itr.hasNext(); ) {
RegressionResult res = itr.next();
if( res != null ) System.out.print( linksbuendigerString(
" " + roundSignificant( res.approxFunction.execute( res.a, res.b, xyArr[i] ), SP ),
" " ) );
}
System.out.println();
}
if( args.length > 20 ) {
System.out.println( "..." );
}
}
}
// Lineare Regression
// y = a + b * x
static RegressionResult calculateLinearRegression( double[] xyArr )
{
if( xyArr == null || xyArr.length < 2 || xyArr.length % 2 != 0 ) return null;
int n = xyArr.length / 2;
double xs = 0;
double ys = 0;
double xqs = 0;
double yqs = 0;
double xys = 0;
for( int i=0; i < xyArr.length; i+=2 ) {
xs += xyArr[i];
ys += xyArr[i+1];
xqs += xyArr[i] * xyArr[i];
yqs += xyArr[i+1] * xyArr[i+1];
xys += xyArr[i] * xyArr[i+1];
}
RegressionResult abr = new RegressionResult();
double xm = xs / n;
double ym = ys / n;
double xv = xqs / n - (xm * xm);
double yv = yqs / n - (ym * ym);
double kv = xys / n - (xm * ym);
abr.rr = Math.min( (kv * kv) / (xv * yv), 1 );
abr.b = kv / xv;
abr.a = ym - abr.b * xm;
abr.titel = "Lin";
abr.formel = "y = " + roundSignificant( abr.a, SP ) + " + " + roundSignificant( abr.b, SP ) + " * x";
abr.approxFunction = new ApproxFunction() {
public double execute( double a, double b, double x ) {
return a + b * x;
}
};
return abr;
}
// Potenzielle Regression
// y = a * x^b
// Regression ueber: ln(y) = ln(a) + b * ln(x)
static RegressionResult calculatePowerRegression( double[] xyArr )
{
if( xyArr == null || xyArr.length < 2 || xyArr.length % 2 != 0 ) return null;
double[] xyArrConv = new double[xyArr.length];
for( int i=0; i < xyArr.length; i+=2 ) {
if( xyArr[i] <= 0 || xyArr[i+1] <= 0 ) return null;
xyArrConv[i] = Math.log( xyArr[i] );
xyArrConv[i+1] = Math.log( xyArr[i+1] );
}
RegressionResult abr = calculateLinearRegression( xyArrConv );
if( abr == null ) return null;
abr.a = Math.exp( abr.a );
abr.titel = "Pow";
abr.formel = "y = " + roundSignificant( abr.a, SP ) + " * x ^ " + roundSignificant( abr.b, SP );
abr.approxFunction = new ApproxFunction() {
public double execute( double a, double b, double x ) {
return a * Math.pow( x, b );
}
};
return abr;
}
// Logarithmische Regression
// y = a + b * ln(x)
static RegressionResult calculateLogarithmicRegression( double[] xyArr )
{
if( xyArr == null || xyArr.length < 2 || xyArr.length % 2 != 0 ) return null;
double[] xyArrConv = new double[xyArr.length];
for( int i=0; i < xyArr.length; i+=2 ) {
if( xyArr[i] <= 0 ) return null;
xyArrConv[i] = Math.log( xyArr[i] );
xyArrConv[i+1] = xyArr[i+1];
}
RegressionResult abr = calculateLinearRegression( xyArrConv );
if( abr == null ) return null;
abr.titel = "Log";
abr.formel = "y = " + roundSignificant( abr.a, SP ) + " + " + roundSignificant( abr.b, SP ) + " * ln(x)";
abr.approxFunction = new ApproxFunction() {
public double execute( double a, double b, double x ) {
return a + b * Math.log( x );
}
};
return abr;
}
// Exponentielle Regression
// y = a * e^(b * x)
// Regression ueber: ln(y) = ln(a) + b * x
static RegressionResult calculateExponentialRegression( double[] xyArr )
{
if( xyArr == null || xyArr.length < 2 || xyArr.length % 2 != 0 ) return null;
double[] xyArrConv = new double[xyArr.length];
for( int i=0; i < xyArr.length; i+=2 ) {
if( xyArr[i+1] <= 0 ) return null;
xyArrConv[i] = xyArr[i];
xyArrConv[i+1] = Math.log( xyArr[i+1] );
}
RegressionResult abr = calculateLinearRegression( xyArrConv );
if( abr == null ) return null;
abr.a = Math.exp( abr.a );
abr.titel = "Exp";
abr.formel = "y = " + roundSignificant( abr.a, SP ) + " * e ^ (" + roundSignificant( abr.b, SP ) + " * x)";
abr.approxFunction = new ApproxFunction() {
public double execute( double a, double b, double x ) {
return a * Math.exp( b * x );
}
};
return abr;
}
// Gespiegelte und verschobene exponentielle Regression
// y = a * ( 1 - e^(-b * x) )
// Approximationsfunktion beginnt bei 0 und strebt gegen den Grenzwert "limit".
// Falls "limit" nicht bekannt ist: Iterativ naehern.
static RegressionResult calculateOneMinusExponentialRegression( double[] xyArr, double limit )
{
double[] xyArrTest = new double[xyArr.length];
for( int i = 0; i < xyArr.length; i+=2 ) {
xyArrTest[i] = -xyArr[i];
xyArrTest[i+1] = limit - xyArr[i+1];
}
RegressionResult abr = calculateExponentialRegression( xyArrTest );
if( abr == null ) return null;
abr.a = limit;
return abr;
}
// Gespiegelte und verschobene exponentielle Regression
// y = a * ( 1 - e^(-b * x) )
// Approximationsfunktion beginnt bei 0 und strebt gegen den Grenzwert "limit".
static RegressionResult calculateOneMinusExponentialRegression( double[] xyArr )
{
final double INCR_FACTOR = 1.001;
double yMax = 0;
if( xyArr == null || xyArr.length < 2 || xyArr.length % 2 != 0 ) return null;
for( int i = 1; i < xyArr.length; i+=2 ) yMax = Math.max( yMax, xyArr[i] );
double lim = searchMaximumFromFunctionFromX( yMax, INCR_FACTOR, xyArr,
new FunctionFromX() {
public double execute( double x, Object helpObject ) {
RegressionResult abr = calculateOneMinusExponentialRegression( (double[]) helpObject, x );
if( abr == null ) return 0;
return abr.rr;
}
});
RegressionResult abr = calculateOneMinusExponentialRegression( xyArr, lim );
if( abr == null ) return null;
abr.titel = "1_E";
abr.formel = "y = " + roundSignificant( abr.a, SP ) +
" * ( 1 - e ^ (-" + roundSignificant( abr.b, SP ) + " * x) )";
abr.approxFunction = new ApproxFunction() {
public double execute( double a, double b, double x ) {
return a * ( 1 - Math.exp( -b * x ) );
}
};
return abr;
}
// Suche den x-Wert fuer den die "FunctionFromX" ein Maximum hat
static double searchMaximumFromFunctionFromX( double xStart, double incrFactor,
Object helpObject, FunctionFromX functionFromX )
{
double x1, x2, xTest;
double y1, y2, yTest;
x1 = x2 = xTest = xStart;
y1 = y2 = yTest = functionFromX.execute( xTest, helpObject );
for( int i = 0; i < 1000000; i++ ) {
xTest *= incrFactor;
yTest = functionFromX.execute( xTest, helpObject );
if( yTest < y1 ) {
x1 = xTest;
y1 = yTest;
break;
}
x2 = x1;
x1 = xTest;
y2 = y1;
y1 = yTest;
}
for( int i = 0; i < 1000000; i++ ) {
xTest = (x1 + x2) / 2;
yTest = functionFromX.execute( xTest, helpObject );
if( y2 >= y1 ) {
x1 = xTest;
y1 = yTest;
} else {
x2 = xTest;
y2 = yTest;
}
if( i > 10 && Math.abs( y2 - y1 ) < 1.0E-12 ) {
break;
}
}
return xTest;
}
private static double[] convertStringArrToDoubleArr( String[] strArr )
{
if( strArr == null || strArr.length <= 0 ) return null;
double[] dblArr = new double[strArr.length];
for( int i=0; i < strArr.length; i++ ) {
strArr[i] = strArr[i].replace( ',', '.' );
dblArr[i] = Double.parseDouble( strArr[i] );
}
return dblArr;
}
private static double roundSignificant( double d, int significantPrecision )
{
if( d == 0 || significantPrecision < 1 || significantPrecision > 14 ) return d;
double mul10 = 1;
double minVal = Math.pow( 10, significantPrecision - 1 );
while( Math.abs( d ) < minVal ) {
mul10 *= 10;
d *= 10;
}
return Math.round( d ) / mul10;
}
private static String linksbuendigerString( String s, String fillStrWithWantLen )
{
if( s != null ) {
int len = s.length();
if( len < fillStrWithWantLen.length() ) {
return (s + fillStrWithWantLen).substring( 0, fillStrWithWantLen.length() );
}
}
return s;
}
static class RegressionResult
{
double a;
double b;
double rr;
String titel;
String formel;
ApproxFunction approxFunction;
}
interface ApproxFunction
{
double execute( double a, double b, double x );
}
interface FunctionFromX
{
double execute( double x, Object helpObject );
}
}
Speichern Sie die gezeigte Java-Klasse in eine Datei mit dem Namen Approximationsfunktionen.java.
Öffnen Sie ein Kommandozeilenfenster, wechseln Sie in das Verzeichnis dieser Datei, und führen Sie zum Kompilieren aus:
javac Approximationsfunktionen.java
Rufen Sie das Programm mit verschiedenen Parametern auf, beispielsweise so (weitere Beispiele siehe nächstes Kapitel):
java Approximationsfunktionen 2 5 3 7 5 11
Beispiele für Approximationsfunktionen
Wenn Sie das Programm zum Beispiel mit den folgenden Parametern aufrufen, erhalten Sie folgende Approximationsfunktionen:
| Übergebene Parameter | Regressionsart | Approximationsfunktion | Excel-Formel |
|---|
| 2 5 3 7 5 11 | Lineare Regression | y = 1 + 2 * x | = 1 + 2 * ZEILE() |
| 2 16 3 54 5 250 | Potenzielle Regression | y = 2 * x ^ 3 | = 2 * POTENZ( ZEILE(); 3 ) |
| 2 5,8 3 7,4 5 9,4 | Logarithmische Regression | y = 3.1 + 3.9 * ln(x) | = 3,1 + 3,9 * LN( ZEILE() ) |
| 1 1,9 2 3,3 4 9,9 9 155 | Exponentielle Regression | y = 1.1 * e ^ (0.55 * x) | = 1,1 * EXP( 0,55 * ZEILE() ) |
| 4 3,7 6 5 18 9 | Gespiegelte exponentielle Regression | y = 10.6 * (1 - e ^ (-0.104 * x)) | = 10,6 * ( 1 - EXP( -0,104 * ZEILE() ) ) |
Wenn Sie die genannten Excel-Formeln in eine Excel-Tabelle zum Beispiel in das A1-Feld einsetzen und anschließend die rechte untere Ecke des A1-Feldes herunterziehen,
werden die y-Werte entsprechend der Excel-Formel zu den jeweiligen Zeilennummern als x-Wert berechnet.
Wenn Sie jetzt alle y-Werte in der A-Spalte markieren, können Sie über
'Einfügen' | 'Diagramm...' | 'Punkt (XY)' | Klick auf mittleres Kurvendiagramm | 'Fertigstellen' ein Diagramm erstellen.
Wenn Sie andere x-Werte benötigen, tragen Sie Ihre x-Werte in die A-Spalte ein, setzen die Excel-Formel daneben in das B1-Feld,
ersetzen in der Excel-Formel "ZEILE()" durch "A1",
ziehen die rechte untere Ecke des B1-Feldes herunter und markieren diesmal die A- und die B-Spalte,
um über 'Einfügen' | 'Diagramm...' | 'Punkt (XY)' | Klick auf mittleres Kurvendiagramm | 'Fertigstellen' das Diagramm zu erstellen.
Falls Excel Werte (z.B. Datum/Uhrzeit) nicht im richtigen Format erkennt und deshalb als String behandelt,
hilft übrigens manchmal ein Speichern der Excel-Datei als unformatierte .csv-Datei und erneutes Laden in Excel.
Wenn Sie Grafiken ohne Excel erstellen wollen, können Sie das Google Chart API testen
(https://developers.google.com/chart).
Durch Anhängen der Parameter an die URL können Sie viele verschiedene Chart- und Grafiktypen erstellen.
Beispielsweise wird die folgende Grafik durch diese URL generiert:
http://chart.apis.google.com/chart?chs=400x200&chtt=100%20*%20(%201%20-%20e^(%20-0,05%20*%20x%20)%20)&chg=20,20&chxt=x,y&chxl=0:|0|20|40|60|80|100|1:|0|20|40|60|80|100&cht=lxy&chd=t:0,1,2,3,5,7,10,13,16,20,25,30,40,50,60,70,80,100|0,4.88,9.52,13.9,22.1,29.5,39.3,47.8,55.1,63.2,71.3,77.7,86.5,91.8,95.0,97.0,98.2,99.3

Wenn Sie dynamisch erstellte Grafiken auf Ihrer Webseite anzeigen wollen, sollten Sie sich das
Google Visualization API
ansehen. Anschauliche Beispiele finden Sie in der
Chart Gallery.
Besonders für mathematisch Interessierte bietet
http://www.wolframalpha.com viele Möglichkeiten:
Sie können dort zum Beispiel Formeln eingeben und sich
Auswertungen
oder auch Kurven-Plots zeigen lassen, zum Beispiel so:
http://www.wolframalpha.com/input/?i=plot+10.6+*+(1+-+e+^+(-0.104+*+x)).
Weitere Java-Bibliotheken zur Kurven- und Chart-Darstellung sind beispielsweise:
JFreeChart,
BIRT (Business Intelligence and Reporting Tools),
JasperReports Java Reporting Library und
Ptplot.
Einige häufig benötigte Formeln
Näherungslösungen zur Suche von Nullstellen
|
| F(x) = 0 | Gesucht ist x für F(x) = 0 |
| F(x) | Funktion von x |
| F’(x) | Ableitung der Funktion von x |
| F’’(x) | Zweite Ableitung der Funktion von x |
| F’(xn) = ( F(xn+d) - F(xn-d) ) / ( 2 * d ) |
Schätzwert der Ableitung der Funktion von x
(falls die genaue Ableitungsfunktion unbekannt ist) |
| xn+1 = xn - F(xn) / F’(xn) |
Rekursive Iterationsformel zur Nullstellensuche nach dem Newton-Verfahren
(Bedingung: F’(xn) ≠ 0, F(xn) * F’’(xn) > 0
und Vorzeichen von F’’(x) wechselt nicht) |
|
| F(x) = 0 | Gesucht ist x für F(x) = 0 |
| yn = F(xn) | |
| xn+1 = x1 - y1 * (x2 - x1) / (y2 - y1) |
Rekursive Iterationsformel zur Nullstellensuche nach der Regula Falsi
(Bedingung: y1 * y2 < 0, also Punkte beiderseits der Nullstelle) |
|
Ableitungsfunktionen
| F(x) | F’(x) |
|---|
| F1(x) + F2(x) | F1’(x) + F2’(x) |
| F1(x) * F2(x) | F1’(x) * F2(x) + F1(x) * F2’(x) |
| F1(x) / F2(x) | ( F1’(x) * F2(x) - F1(x) * F2’(x) ) / (F2(x))2 |
| xn | n * xn-1 |
| x(a/b) | (a/b) * x((a/b)-1) |
| √x | 1 / (2 * √x) |
| ex | ex |
| ax | ln(a) * ax |
| ln(x) | 1 / x |
| log(x) | 1 / (x * ln(10)) |
| x * ln(x) - x | ln(x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | 1 / cos2(x) |
| cot(x) | -1 / sin2(x) |
| arcsin(x) | 1 / √(1 - x2) |
| arctan(x) | 1 / (1 + x2) |
Allgemeine Basisformeln
|
| a0 = 1 | (für a ≠ 0) |
| a(1/2) = √a | |
| a(x/2) = √(ax) | |
| a-x = 1 / ( ax ) | |
| ax+y = ax * ay | |
| ax-y = ax / ay | |
| ax*y = (ax)y | |
| (a * b)x = ax * bx | |
|
| ln(10) * log(e) = 1 | log = Logarithmus zur Basis 10, ln = Logarithmus zur Basis e (= 2,718) |
| ln(x) = log(x) / log(e) | |
| log(x) = ln(x) / ln(10) | |
| ln( ab ) = b * ln(a) | |
| ln( √a ) = ½ * ln(a) | |
| ln( a * b ) = ln(a) + ln(b) | |
| ln( a / b ) = ln(a) - ln(b) | |
|
| sin(α) = cos(90° - α) | |
| tan(α) = sin(α) / cos(α) | |
| cot(α) = 1 / tan(α) | |
| sin2(α) + cos2(α) = 1 | |
| sin(2 * α) = 2 * sin(α) * cos(α) | |
| a / sin(α) = b / sin(β) = 2 * r | Sinussatz (Dreieck-Seite a gegenüber vom Winkel α etc., r = Umkreisradius) |
| a2 = b2 + c2 - 2 * b * c * cos(α) | Kosinussatz (Dreieck-Seite a gegenüber vom Winkel α) |
| (a+b)/(a-b) = tan((α+β)/2) / tan((α-β)/2) | Tangenssatz |
| sinh(x) = ( ex - e-x ) / 2 | |
| cosh(x) = ( ex + e-x ) / 2 | |
| tanh(x) = ( ex - e-x ) / ( ex + e-x ) | |
|
| i | Zinssatz ("Interest per Period"), z.B. 0,03 bei 3% Zinsen |
| q = 1 + i | Zinsfaktor, z.B. 1,03 bei 3% Zinsen |
| K0 | Startkapital ("Present Value") |
| Kn = K0 * qn | Kapital mit Zins und Zinseszins nach n Perioden ("Future Value of Compounded Amount") |
| n = ln( Kn / K0 ) / ln( q ) | |
| Sn = R * (qn - 1) / (q - 1) | Summe der nach n Perioden angesammelten Raten R ("Payment per Period")
bei nachschüssiger Zahlungsweise
(bei Schuldentilgung heißt R Tilgungsrate oder Annuität) |
| Sn = R * q * (qn - 1) / (q - 1) | Summe bei vorschüssiger Zahlungsweise |
|
Weitere Themen: andere TechDocs
© 2008 Torsten Horn, Aachen






